B - Barisan Panda
Nilai "kesenangan" yang disebutkan di soal ini adalah definisi dari inversi pada permutasi sebuah barisan, yaitu banyaknya bilangan pada barisan A di mana A_i > A_j sedangkan i < j, atau bisa juga didefinisikan sebagai banyaknya pasangan pada barisan A yang urutannya terbalik. Batas nilai n yang cukup besar (n <= 200) membuat kita tidak bisa menyelesaikan soal ini dengan mencoba semua permutasi barisan A (brute force) karena banyaknya permutasi dari n elemen adalah n!.
Dynamic Programming
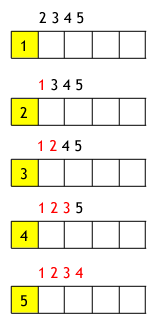 Asumsikan kita memiliki sebuah barisan yang terdiri dari 5 bilangan {1, 2, 3, 4, 5} dan kita ingin mencari ada berapa banyak permutasi dari barisan tersebut yang memiliki tepat 4 inversi.
Bayangkan kita ingin membentuk sebuah permutasi dari barisan tersebut dengan menuliskan bilangan (yang diambil sembarang dari anggota barisan) satu per satu dari kiri ke kanan. Mula-mula kelima slot kita masih kosong, belum ada bilangan yang dituliskan. Tentunya ada lima pilihan bilangan yang bisa kita tuliskan di slot pertama (1..5).
Perhatikan bahwa bilangan apapun yang kita tuliskan akan selalu membentuk inversi dengan semua bilangan yang lebih kecil dan belum dituliskan. Bagaimanapun urutan penulisan bilangan yang belum dituliskan itu nantinya tidak akan mempengaruhi jumlah inversi yang sudah terbentuk oleh bilangan yang sudah dituliskan. Artinya, mencari ada berapa banyak permutasi dari bilangan yang tersisa yang memiliki jumlah inversi tepat k - s (s: jumlah inversi yang sudah terbentuk sebelumnya) menjadi problem baru yang bebas terhadap problem sebelumnya.
Ketika ingin mengambil dan menuliskan satu di antara n bilangan yang belum dituliskan, kita memiliki pilihan:
- mengambil bilangan terkecil
- mengambil bilangan terkecil kedua
- mengambil bilangan terkecil ketiga
- .....
- mengambil bilangan terkecil ke-n
Setiap kali kita mengambil bilangan terkecil ke x, maka jumlah inversi yang terbentuk bertambah sebanyak (x - 1). Artinya, jumlah inversi yang harus dibentuk tersisa sebanyak k - (x - 1). Dengan demikian, kita bisa menuliskan situasi di atas sebagai...
f(n, k) : banyaknya permutasi n bilangan yang memiliki tepat k inversi.
f(n, 0) = 1
f(n, k) = 0 untuk semua k < 0
f(n, k) = f(n-1, k) + f(n-1, k-1) + f(n-1, k-2) + ... + f(n-1, k-(n-1)) untuk semua k > 1
Jumlah state berbeda pada relasi rekurens di atas ada sebanyak O(n.k) sedangkan untuk mengevaluasi satu state diperlukan iterasi sebanyak O(n), sehingga total kompleksitas waktu yang diperlukan untuk menyelesaikan f(n, k) dengan cara ini adalah O(n^2.k).
Untuk mendapatkan kompleksitas waktu O(n.k), kita harus memperhatikan proses pengisian tabel pada metode dynamic programming di atas.
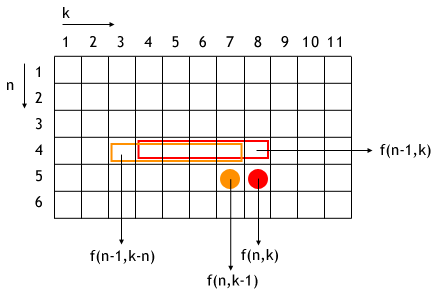
Sebagian besar nilai yang diperlukan untuk menghitung f(n, k) sudah dihitung oleh f(n, k-1), dengan demikian kita bisa memanfaatkannya dengan mengubah persamaan sebelumnya menjadi...
f(n, k) = f(n, k-1) + f(n-1, k) - f(n-1, k-n)
yang memiliki total kompleksitas O(n.k) jika diselesaikan secara dynamic programming.
Statistik Problem B
YES = 2
NO - Wrong Answer = 5
NO - Time Limit Exceeded = 5
NO - Run-time Error = 0
NO - Compile Error = 1
| Solusi C/C++ (oleh Suhendry Effendy) |
#include <cstdio>
#include <algorithm>
using namespace std;
const int mod = 1000007;
const int maxn = 200;
int f[205][20005] = {0};
int main()
{
for ( int n = 1; n <= maxn; n++ ) {
f[n][0] = 1;
for ( int k = 1; k * 2 <= n * (n - 1); k++ ) {
f[n][k] = f[n][k-1] + f[n-1][k];
if ( k >= n ) f[n][k] -= f[n-1][k-n];
f[n][k] = (f[n][k] + mod) % mod;
}
}
int T;
scanf( "%d", &T );
while ( T-- ) {
int n, k;
scanf( "%d %d", &n, &k );
printf( "%d\n", f[n][k] );
}
return 0;
} |
| Solusi Pascal (oleh Eko Wibowo) |
const
modulus = 1000007;
maxn = 200;
var
f:array[1..200,0..20000] of longint;
T, n, k, up : longint;
begin
fillchar(f,sizeof(f),0);
for n := 1 to maxn do
begin
f[n,0] := 1;
up := n * (n - 1) div 2;
for k := 1 to up do
begin
f[n,k] := f[n,k-1] + f[n-1,k];
if (k >= n) then f[n,k] := f[n,k] - f[n-1,k-n];
f[n,k] := (f[n,k] + modulus) mod modulus;
end;
end;
readln(T);
while (T > 0) do
begin
T := T - 1;
readln(n, k);
writeln(f[n,k]);
end;
end. |
|