Operations on Matrix

In this problem, you are given a matrix A of N x M (i.e. A[1 .. N][1 .. M]) and Q queries where each query is one of the following:

• rotate cw r c s
  Rotate the square submatrix A[r .. r+s][c .. c+s] clockwise.
• rotate ccw r c s
  Rotate the square submatrix A[r .. r+s][c .. c+s] counterclockwise.
• reflect x r₁ c₁ r₂ c₂
  Reflect the submatrix A[r₁ .. r₂][c₁ .. c₂] on x-axis.
• reflect y r₁ c₁ r₂ c₂
  Reflect the submatrix A[r₁ .. r₂][c₁ .. c₂] on y-axis.

For example, consider the following matrix of 4 x 5:

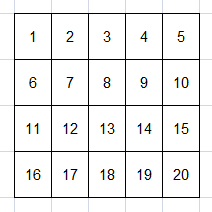
Supposed there are 4 queries, respectively:

• rotate cw 2 1 2
  Rotate the square submatrix A[2 .. 2+2][1 .. 1+2], i.e. A[2 .. 4][1 .. 3] clockwise.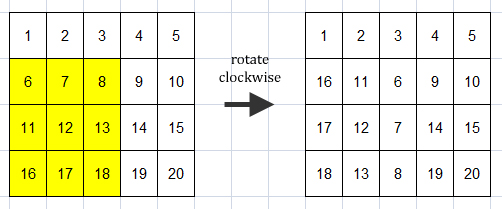
  
• rotate ccw 1 4 1
  Rotate the square submatrix A[1 .. 1+1][4 .. 4+1], i.e. A[1 .. 2][4 .. 5] clockwise.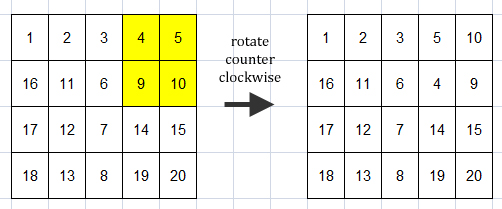
  
• reflect x 2 2 3 5
  Reflect the submatrix A[2 .. 3][2 .. 5] on x-axis.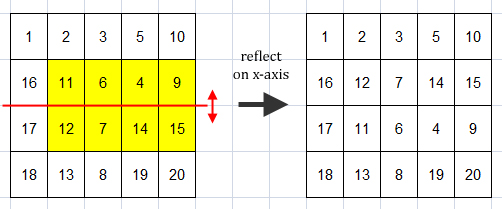
  
• reflect y 2 3 4 5
  Reflect the submatrix A[2 .. 4][3 .. 5] on y-axis.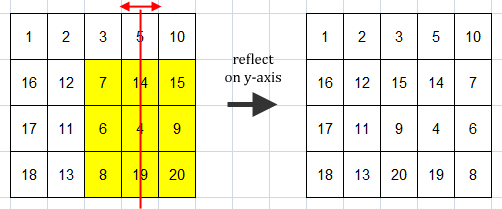
  

Thus, after those queries, the final matrix becomes:

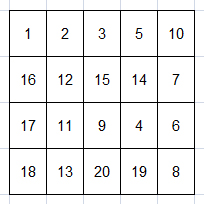
Your task is to output the final matrix after all queries are executed sequentially.

Input

The first line of input contains an integer T (T ≤ 100) denoting the number of cases. Each case begins with three integers N M and Q (1 ≤ N, M ≤ 20; 1 ≤ Q ≤ 20) denoting the matrix size (N x M) and number of queries, respectively. The next N lines, each contains M integers A_i,j (1 ≤ A_i,j ≤ 1,000) representing the intial matrix. The next Q lines, each contains a query with one of the following format:

• rotate cw r c s (1 ≤ r ≤ r+s ≤ N; 1 ≤ c ≤ c+s ≤ M)
• rotate ccw r c s (1 ≤ r ≤ r+s ≤ N; 1 ≤ c ≤ c+s ≤ M)
• reflect x r₁ c₁ r₂ c₂ (1 ≤ r₁ ≤ r₂ ≤ N; 1 ≤ c₁ ≤ c₂ ≤ M)
• reflect y r₁ c₁ r₂ c₂ (1 ≤ r₁ ≤ r₂ ≤ N; 1 ≤ c₁ ≤ c₂ ≤ M)

Output

For each case, output in a line "Case #X:" where X is the case number, starts from 1. The next N lines in each case, each contains M integers each separated by a single space. These integers represent the final matrix after all queries are executed sequentially.

2
4 5 4
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
rotate cw 2 1 2
rotate ccw 1 4 1
reflect x 2 2 3 5
reflect y 2 3 4 5
3 3 2
10 10 10
1 3 9
20 15 17
reflect x 1 1 3 3
rotate cw 1 1 2

Case #1:
1 2 3 5 10
16 12 15 14 7
17 11 9 4 6
18 13 20 19 8
Case #2:
10 1 20
10 3 15
10 9 17