Beautiful Quadruple

In a matrix of integers M, m_i,j denotes the element of the matrix at i^th row and j^th column. A quadruple ⟨a, b, c, d⟩ of M is considered beautiful if and only if (a < b), (c < d), and m_a,c = m_a,d = m_b,c = m_b,d in matrix M.

Given a matrix of integers M, determine how many beautiful quadruple of M there are.

For example, consider the following matrix of 3 x 4:

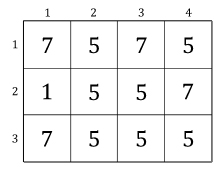
There are two beautiful quadruples, i.e. ⟨1, 3, 2, 4⟩ and ⟨2, 3, 2, 3⟩, as shown in the following figures.

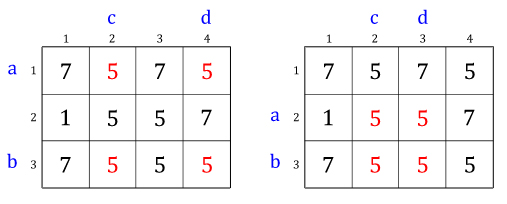
There are no other quadruples which are beautiful, thus, in this example, the output is 2.

Input

The first line of input contains an integer T (T ≤ 100) denoting the number of cases. Each case begins with two integers R and C (2 ≤ R, C ≤ 150) denoting the size of the matrix (row and column respectively). The next R lines each contains C integers m_i,j (1 ≤ m_i,j ≤ 10⁹) representing the matrix's element, respectively for i = 1..R and j = 1..C.

Output

For each case, output in a line "Case #X: Y" where X is the case number, starts from 1, and Y is the output for that particular case.

4
3 4
7 5 7 5
1 5 5 7
7 5 5 5
2 3
1 1 1
1 1 1
4 5
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
3 4
2 8 3 2
2 3 3 2
2 3 3 2

Case #1: 2
Case #2: 3
Case #3: 0
Case #4: 4