ACM-ICPC INC 2008 Qualification

Problem D

Maze Walker

Time Limit: 3s
Given a maze, count how many pairs of distinct cells are there so you can walk from one cell to the other, or vice versa. From each cell you can move in only four directions (North, South, East and West). You cannot move through wall or go outside of the maze's boundary. You can walk from one cell to the other if and only if there's exists a path such that each move is a valid one.

For example,

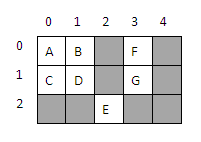
Here you can find 7 pairs of cells: A-B, A-C, A-D, B-C, B-D, C-D and F-G. Note that A-B and B-A are counted as one (they're the same pair). You can walk from A to D (or vice versa) using one of these paths: A-B then B-D, or A-C then C-D. Both of them are valid paths. Meanwhile, you cannot go from D to E because there's no path from D to E.

Input

The first line of input contains an integer T, the number of test cases follow.

Each test case starts with two integer R (1 <= R <= 100) and C (1 <= C <= 100) denoting the number of rows and columns of the maze respectively. The next R lines each contains C characters representing the maze. Walls are denoted by '#' while empty cells are denoted by '.' (dot). There will be no other characters.

Output

For each test case, output in a line the the number of distinct pairs of cells so you can walk from one cell to the other cell.

Sample Input	Output for Sample Input
2 3 5 ..#.# ..#.# ##.## 4 6 ...### ##.##. ###..# ..##.#	7 10