Problem E. Indomie
Problem Author: Felix Halim
Diberikan jumlah indomie tersisa dan panjang antrian, anda diminta untuk menghitung probabilitas Felix mendapat indomie. Soal ini bisa diselesaikan dengan dua pendekatan: kombinatorik dan dynamic programming. Jumlah kombinasi yang bisa terjadi (pada kedua cara) bisa sangat besar dan melebihi batas integer 64-bit, sehingga bisa mengakibatkan overflow. Tipe data double bisa digunakan di soal ini, atau alternatif lain dengan menggunakan BigInteger pada Java.
Kombinatorik
Probabilitas mendapat indomie dapat dirumuskan sebagai:
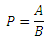
A = jumlah kombinasi di mana Felix mendapatkan indomie.
B = jumlah semua kombinasi yang ada.
Jumlah kombinasi mendapatkan indomie dapat dihitung dengan:
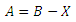
X = jumlah kombinasi di mana Felix tidak mendapatkan indomie.
Felix tidak mendapatkan indomie jika semua stok indomie habis terdistribusi ke semua orang yang mengantri (n orang).
Jika pilihan yang tersedia hanya indomie dan gula (hanya ada dua pilihan), maka sesuai aturan kombinasi (ada berapa cara mendistribusikan s-indomie kepada n-orang), nilai X adalah:
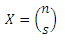
n = jumlah orang yang mengantri di depan Felix.
s = jumlah indomie yang tersedia.
Karena pilihan non-indomie nya ada dua jenis (gula dan beras), maka kombinasi di atas perlu dikalikan dengan 2(n - s). Di mana (n - s) adalah banyaknya non-indomie yang didistribusikan.
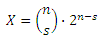
Rumus ini dapat diselesaikan dalam O(s).
Total kombinasi B dapat dihitung dengan menjumlahkan cara mendistribusikan k-indomie kepada n-orang untuk semua k dari 0 s/d s.
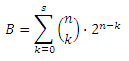
Rumus ini dapat diselesaikan dalam O(s2), namun bisa juga dioptimasi menjadi O(s) dengan memanfaatkan hubungan kombinasi (n,k) dengan (n,k-1).
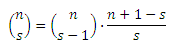
Dynamic Programming
Solusi dynamic programming bisa kita turunkan dari permasalahan ini: banyak cara mendistribusikan maksimal s-indomie kepada n-orang, f(n, s), adalah:
- berikan gula pada orang paling depan, sub-problem nya menjadi: f(n - 1, s) : jumlah orang berkurang, stok indomie tetap.
- berikan beras pada orang paling depan, sub-problem nya menjadi: f(n - 1, s) : jumlah orang berkurang, stok indomie tetap.
- berikan indomie pada orang paling depan, sub-problem nya menjadi: f(n - 1, s - 1) : jumlah orang berkurang, stok indomie berkurang.
Dengan demikian optimal equation untuk problem ini bisa ditulis dalam bentuk:
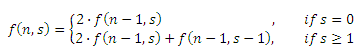
Formula di atas dapat dikomputasi dalam O(n.s).
Sama seperti cara yang digunakan pada pendekatan kombinatorik, probabilitas Felix mendapatkan indomie dapat dihitung dengan membagi jumlah kombinasi Felix mendapat indomie f(n, s - 1) (banyak cara mendistribusikan maksimal s - 1 indomie) dengan jumlah semua kombinasi f(n, s).
Solusi C/C++ (kombinatorik)
oleh Suhendry Effendy
#include <cstdio>
#include <cmath>
using namespace std;
int main()
{
int n, s;
while ( scanf( "%d %d", &n, &s ) == 2 ) {
double x = pow(2.0, n - s);
for ( int i = 1; i <= s; i++ ) x *= (double)(n - i + 1)/i;
double b = pow(2.0, n), v = 1, w = 1;
for ( int i = 1; i <= s; i++ ) {
v *= n - i + 1; w *= i;
b += pow(2.0, n - i) * v / w;
}
printf( "%.5lf\n", (b - x) * 100.0 / b );
}
return 0;
}
Solusi C/C++ (dynamic programming)
oleh Felix Halim
#include <stdio.h>
#include <string.h>
#define MAXN 102
double dp[MAXN][MAXN];
char vis[MAXN][MAXN];
double rec(int n, int s){
if (n<0) return 0;
if (n==0) return 1;
if (vis[n][s]) return dp[n][s]; else vis[n][s] = 1;
return dp[n][s] = 2*rec(n-1,s) + ((s>0)? rec(n-1,s-1) : 0);
}
int main(){
for (int n,s; scanf("%d %d",&n,&s)!=EOF; ){
memset(vis,0,sizeof(vis));
printf("%.5lf\n", 100.0 * rec(n,s-1) / rec(n,s));
}
}
Solusi JAVA (kombinatorik)
oleh Suhendry Effendy
import java.util.*;
public class Indomie {
void solve() {
Scanner scan = new Scanner(System.in);
while ( scan.hasNextInt() ) {
int n = scan.nextInt();
int s = scan.nextInt();
double x = Math.pow(2.0, n - s);
for ( int i = 1; i <= s; i++ ) x *= (double)(n - i + 1) / i;
double b = Math.pow(2.0, n), v = 1, w = 1;
for ( int i = 1; i <= s; i++ ) {
v *= n - i + 1; w *= i;
b += Math.pow(2.0, n - i) * v / w;
}
System.out.printf( "%.5f\n", (b - x) * 100.0 / b);
}
}
public static void main(String[] args) {
new Indomie().solve();
}
}
|