Problem C. Almost Clear
Problem Author: Andoko Chandra
Pembahasan oleh Felix Halim
Diberikan dua buah convex polygon A dan B dan sebuah titik X. Tentukan apakah polygon A bisa terlihat dari titix X? Kalau polygon A tidak terhalang sama sekali oleh polygon B (dilihat dari titik X), maka print "CLEAR". Kalau polygon A terhalang sepenuhnya oleh polygon B maka print "NO VISION". Jika bukan kedua kasus diatas maka print "ALMOST CLEAR".
Semua koordinat yang diberikan adalah berupa bilangan bulat, sehingga tidak perlu takut akan precission-error. Hal yang perlu diperhatikan adalah jumlah titik di masing-masing polygon bisa sebanyak 1000 titik, dan jumlah testcase ada 1000. Artinya, diperlukan algoritma dengan kompleksitas kurang dari O(N2) untuk dapat memecahkan soal ini. Kalau maksa dengan algo O(N2), maka dipastikan dapat TLE :D
Kalau kita analisa lebih dalam, soal ini bisa "disederhanakan" dari Polygon menjadi Garis. Bila kita melihat sebuah polygon dari titik X. Kita cukup mengambil titik paling kiri dan paling kanan dari polygon tersebut (dilihat dari titik X). Di dalam soal diberitahu bahwa polygon A dan polygon B tidak akan intersect dan titik X berada di luar polygon. Perhatikan gambar berikut:
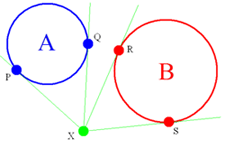 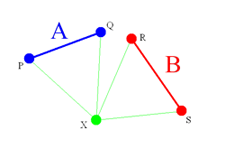
Gambar 1: Menyederhanakan problem dari bentuk Polygon (gambar kiri) menjadi bentuk Garis (gambar kanan).
Jika anda setuju dengan analisis diatas (jika tidak PM ke saya :P), maka permasalahan selanjutnya adalah bagaimana mencari titik paling kiri dan titik paling kanan dari sebuah polygon dengan titik X sebagai titik acuan (kamera)? Cara yang paling mudah adalah dengan test "belok-kiri" atau "belok-kanan". Misalkan kita ingin mencari titik paling kiri dari sebuah polygon dilihat dari titik X. Maka pertama-tama, tentukan titik sembarang di polygon sebagai titik paling kiri (sebut saja titik L), lalu untuk titik lainnya (sebut saja P), test apakah X-L-P belok-kiri? kalau iya, maka titik P berada di sebelah titik L menurut titik X. Maka update-lah titik P sebagai titik paling kiri L, dan cari titik lainnya di polygon sampai habis. Cara ini cuma memerlukan O(N) steps dimana N adalah jumlah titik di polygon. Cara yang sama bisa dilakukan untuk mencari titik paling kanan. Untuk mengetahui belok kiri, kita bisa menggunakan determinant dari 3 titik.
Jadi sekarang kita sudah bisa mencari titik paling kiri dan kanan dari sebuah polygon menurut titik acuan X. Sehingga sekarang kita sudah bisa mengubah Polygon menjadi Garis. Lihat Gambar 1 diatas. Polygon A diubah menjadi sebuah garis P-Q dan polygon B diubah menjadi sebuah garis R-S. Langkah selanjutnya tinggal menentukan apakah garis P-Q tertutup oleh garis R-S?
Hanya ada 3 output: "NO VISION", "CLEAR", atau "ALMOST CLEAR". Bekerja dengan garis jauh lebih mudah daripada bekerja dengan polygon. Kondisi-kondisi apasajakah yang akan menghasilkan "NO VISION", "CLEAR", atau "ALMOST CLEAR"? Untuk lebih jelasnya, lihat gambar dibawah:
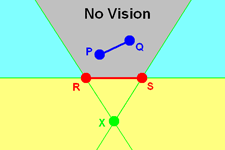
Gambar 2: Print "NO VISION" jika kedua titik P dan Q ada di area dengan background gray. Print "CLEAR" jika kedua titik P dan Q berada di area kuning atau cyan. Print "ALMOST CLEAR" jika kedua kondisi diatas gagal.
Jika kedua titik P dan Q berada di area gray, maka dipastikan polygon A semua tertutup oleh polygon B sehingga outputnya adalah "NO VISION". Untuk mengetahui apakah sebuah titik Y berada di area gray, kita tinggal test X-R-Y harus belok kanan, X-S-Y harus belok kiri, R-S-Y harus belok kiri. Dengan begini kita bisa cek apakah P dan Q berada di area gray atau tidak. Jika ya, maka print "NO VISION" dan selesai.
Jika kedua titik P dan Q berada di area kuning atau cyan, maka dipastikan polygon A tidak terhalang oleh polygon B sehingga outputnya adalah "CLEAR". Untuk mengetahui apakah sebuah titik Y berada di area cyan kita tinggal test X-R-Y harus belok kiri atau X-S-Y harus belok kanan. Untuk mengetahui apakah sebuah titik Y berada di area kuning, maka tinggal test R-S-Y harus belok kanan. Dengan ini kita bisa cek apakah kedua titik P dan Q berada di area cyan atau kuning. Jika ya, maka print "CLEAR" dan selesai.
Jika bukan "NO VISION" ataupun "CLEAR", maka tidak usah pusing lagi, jawabannya pasti "ALMOST CLEAR" :D.
Solusi C/C++
oleh Felix Halim
#include <stdio.h>
struct Point { long long x,y; };
Point A[1000], B[1000], X;
int nA, nB, T, aL, aR, bL, bR;
// return true jika a-b-c belok kiri, false jika bukan
#define left(a,b,c) ((a.x*b.y + b.x*c.y + c.x*a.y - a.y*b.x - b.y*c.x - c.y*a.x) > 0)
int main(){
scanf("%d",&T);
while (T--){
scanf("%d",&nA); for (int i=0; i<nA; i++) scanf("%d %d",&A[i].x,&A[i].y);
scanf("%d",&nB); for (int i=0; i<nB; i++) scanf("%d %d",&B[i].x,&B[i].y);
scanf("%d %d",&X.x,&X.y);
aL = aR = bL = bR = 0;
for (int i=0; i<nA; i++){
if (left(X,A[aL],A[i])) aL = i;
if (!left(X,A[aR],A[i])) aR = i;
}
for (int i=0; i<nB; i++){
if (left(X,B[bL],B[i])) bL = i;
if (!left(X,B[bR],B[i])) bR = i;
}
Point P=A[aL], Q=A[aR], R=B[bL], S=B[bR];
bool gray = !left(X,R,P) && left(X,S,Q) && left(R,S,P) && left(R,S,Q);
bool cyan = left(X,R,Q) || !left(X,S,P);
bool kuning = !left(R,S,P) && !left(R,S,Q);
if (gray){
puts("NO VISION");
} else if (cyan || kuning){
puts("CLEAR");
} else {
puts("ALMOST CLEAR");
}
}
}
Solusi JAVA
oleh Felix Halim
import java.util.*;
public class Poly {
class Point { long x,y; }
// return true jika a-b-c belok kiri, false jika bukan
boolean left(Point a, Point b, Point c){
return (a.x*b.y + b.x*c.y + c.x*a.y - a.y*b.x - b.y*c.x - c.y*a.x) > 0;
}
void solve(){
Scanner scan = new Scanner(System.in);
for (int T = scan.nextInt(); T > 0; T--){
Point[] A = new Point[scan.nextInt()];
for (int i=0; i<A.length; i++){
A[i] = new Point();
A[i].x = scan.nextInt();
A[i].y = scan.nextInt();
}
Point[] B = new Point[scan.nextInt()];
for (int i=0; i<B.length; i++){
B[i] = new Point();
B[i].x = scan.nextInt();
B[i].y = scan.nextInt();
}
Point X = new Point();
X.x = scan.nextInt();
X.y = scan.nextInt();
int aL=0,aR=0,bL=0,bR=0;
for (int i=0; i<A.length; i++){
if (left(X,A[aL],A[i])) aL = i;
if (!left(X,A[aR],A[i])) aR = i;
}
for (int i=0; i<B.length; i++){
if (left(X,B[bL],B[i])) bL = i;
if (!left(X,B[bR],B[i])) bR = i;
}
Point P=A[aL], Q=A[aR], R=B[bL], S=B[bR];
boolean gray = !left(X,R,P) && left(X,S,Q) && left(R,S,P) && left(R,S,Q);
boolean cyan = left(X,R,Q) || !left(X,S,P);
boolean kuning = !left(R,S,P) && !left(R,S,Q);
if (gray){
System.out.println("NO VISION");
} else if (cyan || kuning){
System.out.println("CLEAR");
} else {
System.out.println("ALMOST CLEAR");
}
}
}
public static void main(String[] args){
new Poly().solve();
}
}
|