Problem B. Panda Land 5: Panda Programming Language
Problem Author: Evan Leonardi
Diberikan beberapa fungsi beserta graph dependensinya pada sebuah program, anda diminta untuk mengatur susunan fungsi tersebut dengan cost seminimum mungkin sehingga program tersebut dapat dikompile. Sekilas soal ini terlihat sangat susah (meskipun memang termasuk susah di antara soal yang lain), karena kombinasi dan urutan pemindahan yang bisa dilakukan cukup banyak. Batasan nilai N sebesar 18 membuat soal ini tidak bisa diselesaikan secara bruteforce O(N!) dan memaksa kita mencari solusi yang lebih efisien.
Berikut ini adalah ilustrasi untuk sample input #2:
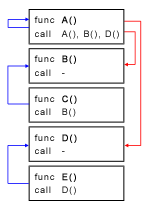 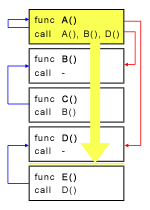 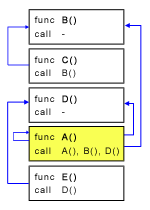
Pemindahan A ke bawah D secara langsung pada gambar di atas dapat diuraikan menjadi beberapa pemindahan bertahap (meloncati satu fungsi saja), yaitu: pindahkan A ke bawah B, dilanjutkan ke bawah C, dan setelah itu ke bawah D. Total cost yang digunakan adalah: (A * B) + (A * C) + (A * D) = A * (B + C + D).
Jika diperhatikan, pemindahan dengan meloncati satu fungsi saja itu sama dengan menukar posisi kedua fungsi tersebut (memindahkan A ke bawah B adalah sama dengan memindahkan B ke atas A). Jadi tidak masalah apakah kita ingin memindahkan sebuah fungsi ke bawah atau ke atas, karena pasti ada langkah equivalent untuk arah yang sebaliknya. Sehingga, untuk menyelesaikan soal ini kita bisa memfokuskan pada pemindahan ke satu arah saja (ke bawah atau ke atas).
Pada contoh di atas, langkah equivalent untuk pemindahan A ke bawah D adalah: pindahkan B ke atas A (B * A), kemudian pindahkan C ke atas di antara A dan B (C * A), dan terakhir pindahkan D ke atas di antara A dan C (D * A).
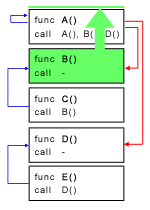 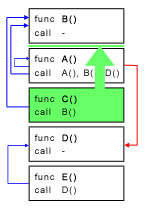  
Berikutnya, kita selesaikan problem ini dengan mencoba semua kombinasi pemindahan fungsi (di penjelasan ini kita akan menggunakan pemindahan ke atas). Mulai dari state awal (semua fungsi belum dipindahkan), pilih salah satu fungsi yang belum dipindahkan (coba semua) dan pindahkan fungsi tersebut ke atas di bawah fungsi-fungsi yang sudah dipindahkan sebelumnya. Dengan cara ini, semua kombinasi urutan pemindahan bisa kita coba.
Contoh pemindahan fungsi dan cost-nya:


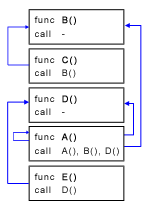
Ilustrasi perpindahan minimum pada sample input #2:





Pencarian cost minimum dengan mencoba semua kombinasi seperti ini bisa dinyatakan dengan state:
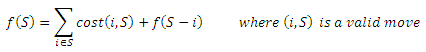
S = set fungsi yang belum dipindahkan.
i = fungsi i, member dari set S.
f(S) = cost minimum untuk mengatur ulang posisi fungsi pada state S.
cost(i, S) = cost untuk memindahkan fungsi i pada state S.
fungsi i boleh dipindahkan (valid) hanya jika semua fungsi yang dipanggilnya sudah dipindahkan terlebih dahulu (tidak ada dalam S).
State di atas bisa diselesaikan dengan dynamic programming. Gunakan bit masking untuk mengimplementasikan set S pada program (0:tidak ada dalam set; 1:ada dalam set). Semua nilai dari cost(i, S) bisa digenerate dalam O(N . 2N), sehingga setiap pemanggilannya hanya O(1). note: 2N adalah ukuran untuk semua kombinasi set S. Dengan demikian, total kompleksitas yang diperlukan untuk f(S) adalah O(N . 2N).
Solusi C/C++
oleh Suhendry Effendy
Felix Halim memodifikasi bagian deteksi cycle (-1) sehingga menjadi lebih efisien
(sebelumnya menggunakan metode Floyd Warshall).
#include <cstdio>
#include <algorithm>
using namespace std;
#define REP(i,n) for(int (i)=0,_n=(n);(i)<_n;(i)++)
const int max_n = 18;
const int inf = 1000000000;
int n, t, u;
int w[max_n];
int p[max_n];
bool call[max_n][max_n];
int sum[1<<max_n];
int need[max_n];
int dp[1<<max_n];
bool allow(int i, int bit) { return (need[i] & bit) == 0 && ((1<<i) & bit); }
int cost(int i, int bit) { return w[p[i]] * sum[bit & ((1<<i)-1)]; }
int f(int bit) {
if ( dp[bit] != -1 ) return dp[bit];
int &ret = dp[bit] = inf;
REP(i,n) if ( allow(i,bit) )
ret = min(ret, cost(i,bit) + f(bit & ~(1<<i)));
return ret;
}
int main(){
int T;
scanf( "%d", &T );
while ( T-- ) {
memset(call,false,sizeof(call));
memset(sum,0,sizeof(sum));
memset(need,0,sizeof(need));
memset(dp,-1,sizeof(dp)); dp[0] = 0;
scanf( "%d", &n );
REP(i,n) scanf( "%d", &w[i] );
REP(i,n) {
scanf( "%d", &t );
REP(j,t) {
scanf( "%d", &u );
if ( i != u-1 ) call[i][u-1] = true;
}
}
REP(i,n) scanf( "%d", &p[i] ), p[i]--;
REP(i,n) REP(bit,1<<n) if ( bit & (1 << i) ) sum[bit] += w[p[i]];
REP(i,n) REP(j,n) if ( call[p[i]][p[j]] ) need[i] |= (1 << j);
int ans = f((1<<n)-1);
printf( "%d\n", ans == inf ? -1 : ans );
}
return 0;
}
Solusi JAVA
oleh Suhendry Effendy
import java.util.*;
public class Panda {
final int max_n = 18;
final int inf = 1000000000;
int n, t, u;
int[] w = new int[max_n];
int[] p = new int[max_n];
boolean[][] call = new boolean[max_n][max_n];
int[] sum = new int[1<<max_n];
int[] need = new int[max_n];
int[] dp = new int[1<<max_n];
boolean allow(int i, int bit) { return (need[i] & bit) == 0 && ((1<<i) & bit) != 0; }
int cost(int i, int bit) { return w[p[i]] * sum[bit & ((1<<i)-1)]; }
int f(int bit) {
if ( dp[bit] != -1 ) return dp[bit];
int ret = inf;
for ( int i = 0; i < n; i++ ) if ( allow(i,bit) )
ret = Math.min(ret, cost(i,bit) + f(bit & ~(1<<i)));
return dp[bit] = ret;
}
void solve() {
Scanner scan = new Scanner(System.in);
int T = scan.nextInt();
while ( T-- > 0 ) {
for ( boolean[] i : call ) Arrays.fill(i,false);
Arrays.fill(sum,0);
Arrays.fill(need,0);
Arrays.fill(dp,-1); dp[0] = 0;
n = scan.nextInt();
for ( int i = 0; i < n; i++ ) w[i] = scan.nextInt();
for ( int i = 0; i < n; i++ ) {
t = scan.nextInt();
for ( int j = 0; j < t; j++ ) {
u = scan.nextInt();
if ( i != u-1 ) call[i][u-1] = true;
}
}
for ( int i = 0; i < n; i++ ) {
p[i] = scan.nextInt();
p[i]--;
}
for ( int i = 0; i < n; i++ )
for ( int bit = 0; bit < (1<<n); bit++ )
if ( (bit & (1 << i)) != 0 ) sum[bit] += w[p[i]];
for ( int i = 0; i < n; i++ )
for ( int j = 0; j < n; j++ )
if ( call[p[i]][p[j]] ) need[i] |= (1 << j);
int ans = f((1<<n)-1);
System.out.println( ans == inf ? -1 : ans );
}
}
public static void main(String[] args) {
new Panda().solve();
}
}
|